Volatility vs. Average True Range (ATR)

Differences and Similarities When Placing Stops and Calculating Position Sizes

The utilization of average true range (ATR) by systematic trend following CTAs to determine position sizes and stop levels is an effective and valuable means of normalizing expected P&L.

Additionally, incorporating ATRs helps with performance analysis as each trade can be evaluated in ATR-terms, providing a standardized framework. The late Van Tharp has authored one of the best books on this topic.

In this article, we’ll aim to outline certain frailties related to the use of position-sizing and stop-placement parameters. We’ll also compare the pros and cons of the commonly used ATR method to an alternative method that’s based on annualized standard deviation, or volatility.

We thank

George Coyle

for his contribution and valuable comments on everything that follows.

Let’s start.

CTAs typically undertake the following calculations to determine stops and exit levels:

1. Calculate the true range (TR) using price differences, adjusted for overnight price gaps

2. Compute an average of the TR to arrive at the ATR

3. Assign a multiplier to the ATR to find stops and exits

These calculations raise a couple of questions. For example, regarding step 1 above, why not use percentages instead of price differences, i.e., High/Low-1 instead of High-Low to get a daily percentage TR? This would normalize the TR for big price swings, such as those observed in natural gas and power markets in Q1 and Q2 of 2022. When news outlets report that the Dow is up 100 points, it becomes kind of irrelevant unless one knows the level of the Dow (denominator). A percentage move normalizes to any price level.

Example

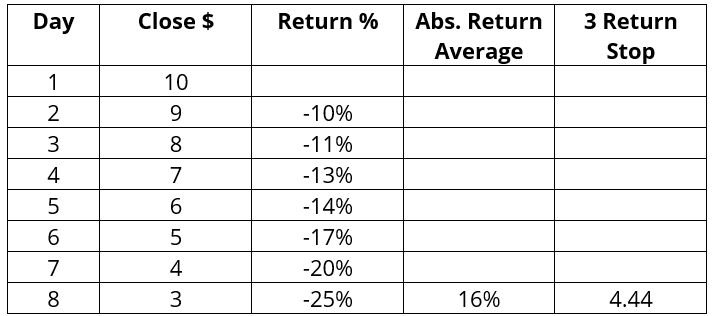
In the table below, the market moves from $10 to $3 over 8 trading days. The change each day is $1 (TR). Therefore, the ATR is also $1.

Assume our trend following model signals to open a short position at a closing price of $3. If we risk 3 ATRs, our initial stop would be at $6 and thus 100% away from the last price of $3.

Now consider this example with the same data but percentages.

The percentage method normalizes the changes for the price level and thus sets the stop based on the average of the relative changes, expressed in percentage terms. The result is a drastically different stop level:

16% * $3 = $0.48 and $3 + $0.48 * 3 = $4.44

This stop sits 48% as opposed to 100% above the last closing price. All else being equal, the position size would therefore be more than twice as large using the percentage method.

If prices moved the other way (start at $3 and end at $10), the corresponding stops for a long position would be $7 using the ATR method and $4.30 with the percentage method. This accounts for the fact that 1/3 is a lot different than 1/9.

In contrast to the previous example of declining prices, the percentage method now places the stop further away from the entry price, and the ATR method would produce a much larger position size.

The inconsistency is evident.

While the aforementioned examples are extreme, it seems reasonable to assert that the ATR method sometimes risks too little, and sometimes too much, with a path-dependency on recent price levels. Moreover, the examples suggest that utilizing the percentage method would be more consistent with respect to calculating initial stop levels and position sizes.

Sidenote: As an alternative to risking x times the %TR with the percentage method, we could calculate a standard deviation of the daily %TR and then determine the stop level by using a standard deviation multiplier. For example, let’s say the 20-day average of the %TR is 1% and the 20-day standard deviation of the %TR is 0.25%. If we wanted 3 standard deviations (99.7% confidence interval per statistics) we’d calculate the ATR stop multiplier by taking 1% + (3*0.25%) = 1.75%. This would then be multiplied by the price at trade inception to find the stop level and position sizes would be calculated as usual.

What’s better? Whereas ATR multipliers are determined with discretion using backtests, standard deviations have a foundation in statistics. As we know, these are bell curve dependent and the assumption is that the observed volatility will persist – but that’s the basic assumption anyway. While we loathe the bell curve, we also assume the ATR as measured at trade inception will persist.

Negative Prices

One inconvenient side effect of the percentage method is that we would need to change our historical continuous contract time series. When we create continuous futures time series, back adjusted for price differences at the time of the rollover, we can (and do) end up with negative prices. With negative prices, our ATR approach remains functional, whereas the percentage method does not. This issue can be resolved by shifting the entire time series up into positive territory. However, doing so means that the last price of our time series will no longer match the last price of the current contract.

Alternatively, one could consider reversing the sign of negative numbers since they also work “backward” (see table below), or maybe use an absolute value of the percentage changes and take the average of that.

However, the percentage method would still leave us with the problem on the 0 placeholder, and the inability to use 0 in a fraction. While we can think of workarounds for this issue, this article hopefully showed that both methods have their pros and cons, if not in calculation, then in other ways. For example, an ultra-low ATR will cause the system to trade a very large notional amount of something (with the workaround being minimum ATRs per market), whereas the percentage method may result in more consistent risk-taking.

We hope this article provides food for thought. Sometimes, the most essential building blocks of a systematic trading program become the most interesting.