Bend It Like a Trend Follower: Mastering Market Convexity

Introduction

In recent client visits, a recurring theme emerged: the appeal of Trend Following strategies and their distinct return profiles. These discussions highlighted a broader curiosity about the mechanics of financial strategies and their impacts on returns, particularly the concept of convexity.

In mathematical finance, convexity describes the presence of non-linear relationships within a financial model. Essentially, when the price of an underlying variable shifts, the resulting change in the price of an output is not linear but is influenced by the second derivative—or higher-order terms—of the function used in the model. This means the model does not exhibit a flat, but rather a curved geometric shape. The extent of this curvature, which illustrates the degree to which the model deviates from linearity, is referred to as convexity.

While often associated with options trading, convexity plays a crucial role in the lesser-discussed realm of Trend Following. This article explores how convexity manifests in Trend Following strategies, providing insight into the parameters driving their unique risk-return dynamics.

Understanding Convexity in Options

Options trading is renowned for its convex payoff structure, arising from the non-linear relationship between the option's price and the underlying asset's price movements. While this article focuses on a few key factors—delta, gamma, and volatility—it’s important to understand that options pricing and convexity are influenced by a broader set of sensitivity measures known as the Greeks. These factors not only affect option prices but can also interact with each other in complex ways, further shaping the option's risk-return profile.

• Intrinsic and Time Value: An option's price is comprised of intrinsic value—its value if exercised immediately—and time value, which decreases as the option nears its expiration. This decline in time value contributes to the option's non-linear pricing characteristics.

  Chart 1: Visualizes how the value of a call option changes with the underlying asset's price, depicting both the intrinsic value and the total option value for different times to expiration (T). The x-axis represents the range of prices for the underlying asset, and the y-axis shows the value of the option.

  

• Delta and Gamma: These derivatives measure how the option's price changes in response to movements in the underlying asset. Delta indicates the rate of change for each unit move in the underlying asset. Gamma, the rate at which delta changes, further accentuates the curvature in the option's response to market movements.

  Chart 2: Illustrates Delta and Gamma as functions of the underlying asset's price, where Delta progresses in an 'S' curve, increasing sensitivity around the at-the-money point, and Gamma peaks, showcasing the highest convexity in the option's price response to market movements.

  

• Leverage and Volatility: Options provide leverage, amplifying returns from minor movements in the underlying asset. Their sensitivity to market volatility also plays a critical role; as volatility increases, so does the option's time value, enhancing the likelihood that the option will end up in-the-money at expiration.

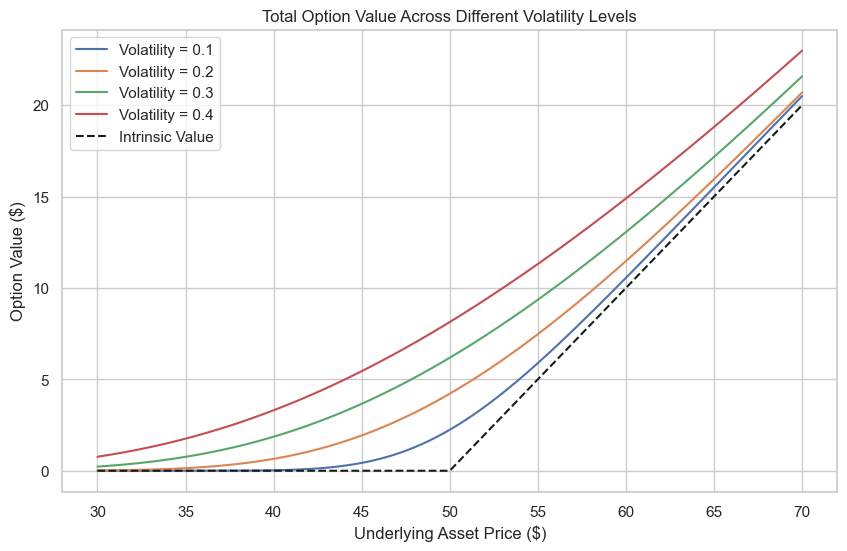
  Chart 3: Each curve represents the option's value at different levels of volatility, illustrating that higher volatility increases the probability of the option ending in the money, thereby increasing its expected payoff.

  

Exploring Convexity in Trend Following

Unlike options trading, which inherently features convexity through mathematical models like the Black-Scholes formula, the convexity in Trend Following strategies emerges from the execution and sizing of trades rather than inherent properties of financial instruments. This section will explore how strategic decisions within trend following create a convex payoff structure. The shown strategy uses a single market and only serves as an illustration. The experienced Trend Follower will surely spot some elements where this strategy is lacking. Despite these shortcomings and its roughness, even this simple example captures the basic aspects of Trend Following.

Mechanical Convexity: At its core, Trend Following benefits from what could be termed 'mechanical convexity.' This form of convexity isn’t derived from derivatives or complex financial instruments but from a simple yet powerful strategy design. Trend followers capitalize on large, sustained movements in the market, which allows them to ride winners significantly while cutting losses quickly. This strategy leads to payoffs that are not linearly related to market moves but accelerate profits as trends strengthen.

Chart 4: To visually represent this, Chart 4 displays the joint and single densities of market returns versus strategy returns. The strategy's ability to capture right tail events is highlighted by a distinct blue cloud to the upper right, which visually represents the higher returns achieved during significant market uptrends.

Chart 5: A scatterplot with a polynomial fit demonstrates the convex nature of the strategy. The less steep left tail indicates that our strategy has limitations in capturing short-term negative trends. Due to the low number of observations in the tails for this market, the confidence intervals, shaded in red, become wider for large absolute returns. To reduce the element of luck and produce statistically significant samples, Trend Following strategies typically spread their bets across many markets.

Position Sizing: Position sizing is a cornerstone in managing the convexity effectively within Trend Following strategies. It is finely tuned to maximize gains while minimizing risks:

• Adapting to Volatility: Position sizes are adjusted according to the prevailing market volatility. This method helps manage temporary drawdowns effectively, allowing traders to maintain their positions without facing significant losses.

• Loss Management: By exiting trades that do not perform as expected at a controlled loss, traders can preserve capital to invest another day. This tactic is crucial in avoiding the trap of holding onto losing positions too long, hoping for a turnaround.

• Dynamically Adjusting to Market Changes: Adapting position sizes as volatility shifts ensures that exposure remains optimized for current market conditions.

• Pyramiding: This involves adding to a winning position in increments. As a trade moves favorably, increasing the investment in that position can magnify the returns on successful trades without proportionately increasing the risk.

The effectiveness of position sizing and its impact on convexity is evident across various Trend Following strategies, regardless of the specific entry signals used.

Chart 6: Strategy returns for different signals and position sizing strategies highlight that there can be considerable variation within a single market strategy. However, overall convexity prevails, demonstrating the strategy's ability to profit more significantly from larger market moves than it loses from smaller ones.

Long-Term Engagement: Trend Following strategies often operate without a predefined endpoint, allowing traders to capitalize on long-term trends as long as they persist. This open-ended nature is crucial for compounding returns over time. Trend Following is not about quick gains but about staying engaged with the market to capture large trends over months or years. This contrasts sharply with the fixed lifecycle of options, where timing and expiration limit strategic flexibility.

Chart 4: This plot illustrates the relationship between trade duration and profitability. It shows that trades held longer, aligned with enduring trends, tend to be more profitable, highlighting a positive skew in return distribution. The longer a system can maintain a position in a favorable trend, the higher the likelihood of capturing substantial returns. For this specific Trend Following model, the average number of days held for winning trades is 26.58 days, while the average number of days held for losing trades is only 6 days.

Leverage and Volatility

Similar to options trading, Trend Following strategies often utilize leverage when trading futures. The profitability of these strategies is closely tied to the volatility of the underlying asset. Trend Following tends to be effective when there are sustained market movements, either upward or downward, that align with the strategy’s established timeframe. For an extensive analysis, see “The Convexity of Trend Following” in the Hedge Fund Journal.

Conclusion

Both Trend Following and options trading significantly leverage convexity, albeit with distinct mechanisms and implications. This article has explored how strategic nuances influence the convexity in these financial models, highlighting the necessity for traders and investors to comprehend these dynamics for effective strategy implementation. As we introduce the Takahē Global Markets fund, we are excited to offer an investment opportunity that maximizes the advantages of Trend Following. We encourage those interested in this high-octane approach to visit our website at takahe.capital for more information and to join us in this promising venture.